素数生成プログラム エラトステネスの ふるいは素数を見つける方法の1つです。 次がエラトステネスのふるいによって素数を生成するプログラムです。 >>> n =int (input ("n以下の素数と個数を表示。 n=")) 実行してみると、nの値を尋ねられるので100と代入し プログラミング初心者のための簡単アルゴリズム入門素数を数えて落ち着くんだ 青木です。 paizaラーニング 担当のエンジニアです。 人間、どうしても素数を数えて落ち着きたいときってあると思います。 順に数えてくと、2, 3, 5, 7, 11, 13, 17, 19, 23, 29エラトステネスえらとすてねすEratosthenes(前275ころ―前194ころ) ヘレニズム 時代の最初の体系的 地理学者 。 アフリカの キレネ に生まれる。 もっとも多能多芸な人物で、ベータBeta(第二の人、アルファに次ぐ人の意)と称された。 プトレマイオス3世に招聘 (しょうへい)されて、当時の世界文化の中心地 アレクサンドリア の 図書館 長を務めた。 数学では 素数

ピラミッド計算その4 Sakurai Susumu Website
エラストテネスのふるい
エラストテネスのふるい- エラトステネスの篩 世の中には頭のいい人がいるもので、エラトステネスの篩という素数判定アルゴリズムがあります。 とても単純明快パワフル。 アルゴリズムをWikipediaから引用してみます。 ステップ 1 探索リストに2からxまでの整数を昇順で入れるErastosthenes の 篩 を使用するバージョン3( Paul Tomblinに感謝): Java 15を使用していますか? List を返し、 ArrayList を使用しないでください。 int を返す必要がある場合、処理の最後にListを int 変換することでそれを行うことができます



13日目 エラトステネスの篩 ふるい を知ってますか 30日間1日1本マクロ生活 わたしの日常に価値はありますか
%2 ユークリッドの世界 『エラトステネスの仮説』 二千年前の、エジプトのアレキサンドリアには大きな図書館があっ 前回の while文 に引き続いて、繰り返しの動作を行う構文について学習していきます。while文 の他に、もうひとつ、繰り返し処理を実現する方法が for文 です。 「入力した数値を加算して、ある所で入力値の平均値を求める」課題のように参加者の人数がプログラムを実行する度に毎回変わ 今日の料理 ニラを入れすぎた 概要 素数のリストを作成する際に、エラトステネスのふるいが有名だが、それを改良した「アトキンのふるい」というものがある。今回は、他のコードを参考にしながら、自前で実装してみて、思ったことを書き残しておきたいと思う。
Pythonエラトステネスの篩というアルゴリズムを使えば素数を簡単に探すことができます。 そのアルゴリズムをPythonで実装してみました。 ソースコードは以下のとおりです。 View the code on Gis 続きを読む "Pythonエラトステネスの篩を使ってPythonで素数を探す" エラトステネスの篩 (エラトステネスのふるい、 英 Sieve of Eratosthenes) は、指定された 整数 以下の全ての 素数 を発見するための単純な アルゴリズム である。 古代ギリシア の科学者、 エラトステネス が考案したとされるため、この名がついている。 今日は、2 以上 n 以下の自然数の中から素数を抽出(素数以外を排除)する C によるアルゴリズムについてです。まず、「自然数 p ( > 1 ) が 1 と p の他に正の約数を持たない場合、p を素数という。」です。そして、簡単に言うと、自然数の配列をふるいに見立てて素数以外を排除し
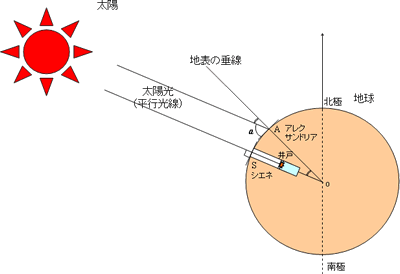
エラトステネスの篩の素数判定プログラム (c#) スポンサーリンク ※サイト運営にサーバーは 必須 です※ ~このサイトも エックスサーバー を使用しています~ 目次 hide 1 はじめに 2 1:単純なエラトステネスのふるい 3 2:√Nで、篩を止める 4 3奇数 紀元前3世紀、ヘレニズム時代のエジプトで活躍した人物、 エラトステネス。 ギリシャの都市に誕生した彼は、エジプトのファラオの命により、当時最高峰の英知が集結していた図書館の館長を長年にわたって務めました。 科学的な視点を用いてあらゆる学問に精通していた彼は、やがエラトステネス • エジプトのシエネでは、夏至の正午に太陽が真上に来る。 • アレクサンドリアでは真上からε = 75°の角度と測定。 • シエネはアレクサンドリアから真南に約800kmである。 Sun Syene Alexandria C r s これより、地球の半径 。現代 – p2/8




ギリシャとサラブレッドの関係性の口コミ 評判 競馬予想winners



エラトステネスが求めた地球の大きさ サラリーマン 宇宙を語る
エラトステネスの篩(ふるい) とは, n n n 以下の素数を全て見つけ出す高速な方法です。 エラトステネスのふるいの概要と,愚直に計算するよりも速いこと(計算量が O ( n log log n) O (n\log\log n) O(nloglogn) であること)を紹介します。 目次 愚直な エラトステネスの篩 in C C Project Eulerの素数を扱う問題で必要になったので、エラトステネスの篩を実装してみた。 実装した関数 sieve は、上限 max までの数の中で素数であるものを探し、対応する IsPrime の要素を true にする。 エラトステネスの篩というのは n 以下の整数の素数を求めるアルゴリズムです。 原理自体はとても簡単で、たくさんの数を用意して、次にひたすら割り続けます。 割ることができた数は振い落とします。 以下では 1 から 169 の数を用意して 1, 2, 3, 5, 7, 11




エラトステネスとはどんな人物 簡単に説明 完全版まとめ 歴史上の人物 Com



地球の概観
エラトステネスの篩 エラトステネスでググったら出てきて、さすがにカオス過ぎて笑ってしまいました。 エラトステネスの篩というのは n 以下の整数の素数を求めるアルゴリズムです。 原理自体はとても簡単で、たくさんの数を用意して、次にひたすら割り続けます。 割ることができた数は振い落とします。 以下では 1 から 169 の数を用意して 1, 2, 3, 5, 7, 11, 13エラトステネスが考案した 素数 検出法。 その方法は,合成数を順次 ふるい にかけるように落して,任意の正の 整数 をこえない素数を見出すことにある。 まず1は素数でないから落す。 次に2と N の間にあるすべての正の整数を大きさの順に並べる。これでわかりますよね。 5000スタジアが地球全周の360分の72、つまり50分の1になり、地球全周は5000×50=スタジアになる、これがエラトステネスの求めた地球の大きさです。 1スタジオンを184mとしますと、4万6000kmです。 現在分かっている地球一周の長さは4万kmです。 つまり、彼の求めた地球の大きさは実際に地球より15%程度大きいだけでした。 15%も誤差が




Ctc これからの世界を読み解く 数学体感教室 朝日新聞デジタル



Python 素数判定の計算量を減らしていく 数学 コジマノテック
This is animation of the sieve of Eratosthenes, an algorithm for finding prime numbersいつもと趣向を変えて、素数のビジュアライズをしてみました。眺めているとC\DATA\Java2\Dos>java Matsosu 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 97 Press any key to exit (Input "c" to continue)現在では、子午線の長さは約 4 万 km と分かっていますが、エラストテネスの計算結果はそれより 15 %ほど大きいだけでした。 日本ではじめて地球の大きさを測ったのは、江戸時代の元商人で天文学者、地理学者、そして測量家でもあった伊能忠敬(いの




ユニーク 素数 の 覚え 方 画像コレクション



エラトステネスが求めた地球の大きさ サラリーマン 宇宙を語る
衛星による測定で48,000kmであるので、エラストテネスとの誤差は2~4%である。 コロンブスが西回りで帰港したからといって、地球が丸いことの証明にはならない。地球 がベーグルの形状でも西回りで戻って来られる。 ポアンカレ予想(Poincare Conjecture) 素数を見つける方法の1つであるエラトステネスの篩(ふるい)をご紹介します! エラトステネスの篩とは? エラトステネスの篩とは素数は「約数が2つしかない(1と自分自身の2つ)」という性質を利用して素数を見つける方法です。 まずは動画をご紹介。 エラトステネスが地球を測った方法 紀元前240年(約00年前)、ギリシャの天文学者エラトステネスは、地球の大きさをはじめて測量した人物として知られています。 その方法は、 二つの遠く離れた街にできる影の角度と街の距離の情報から地球の円周を求める というものでした。 彼の推定した地球の精度は00年前にも関わらず、脅威の精度で地球の大きさを
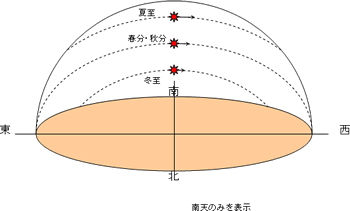



地球を測 はか る 科学夜話 学びの場 Com




プログラミング




プログラミング




Primepi Wolfram言語ドキュメント
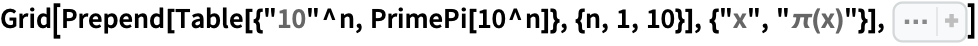



Primepi Wolfram言語ドキュメント



13日目 エラトステネスの篩 ふるい を知ってますか 30日間1日1本マクロ生活 わたしの日常に価値はありますか




エラトステネスとはどんな人物 簡単に説明 完全版まとめ 歴史上の人物 Com



地図と一秒の世界



エラストテネスの夕方




エラトステネスの篩の計算量を実験で確認する Qiita
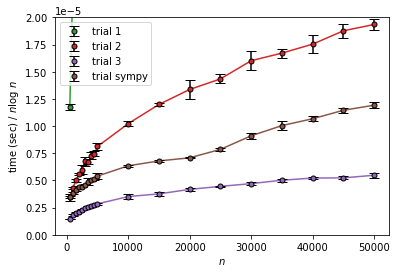



エラトステネスの篩の計算量を実験で確認する Qiita




年周視差 Wikipedia



地球の半径を測る




高校世界史b 自然科学の発達 映像授業のtry It トライイット




Primepi Wolfram言語ドキュメント



地球の概観




年周視差 Wikipedia




Haskell 素数判定 試し割り エラトステネスの篩 Web備忘録




エラトステネス Wikipedia



緯度 経度の 1度はどれくらいの長さがあるのか Wingfield Since1981



Algorithm C




Leo S Blog




エラトステネスの篩 英丸くんの日常




パンとサーカスとその他もろもろの日々 15
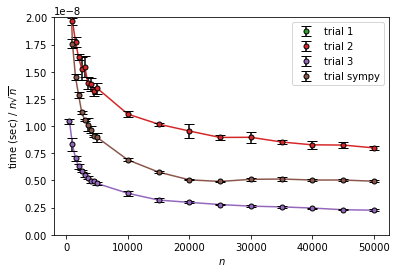



エラトステネスの篩の計算量を実験で確認する Qiita



地図と一秒の世界




Prime Wolfram言語ドキュメント




数学的帰納法によるプログラミングを修得するためにf 代数を攻略する Bitterharvest S Diary



地球を測 はか る 科学夜話 学びの場 Com




Prime Wolfram言語ドキュメント



エラストテネスとクレーターチェン



年03月 令和元年 から のプログラミング




アーカイブ 08 31 17 日本今日



地球を測 はか る 科学夜話 学びの場 Com




地球球体説 Wikipedia



地球の半径を測る
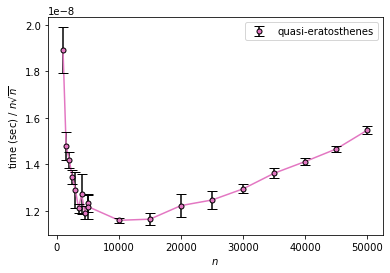



エラトステネスの篩の計算量を実験で確認する Qiita



ユニーク 素数 の 覚え 方 画像コレクション




素数 たかしの愛した算数学



素数
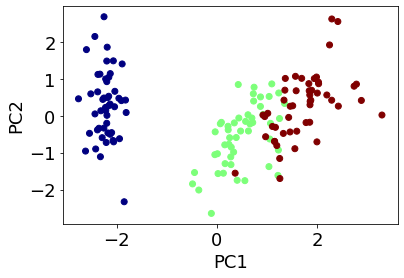



年03月 令和元年 から のプログラミング
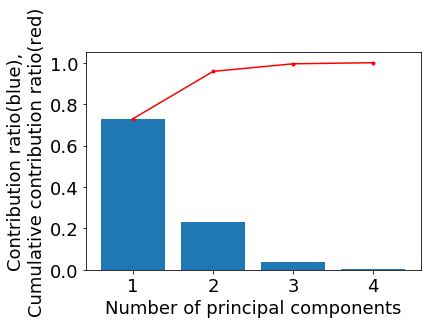



年03月 令和元年 から のプログラミング




地図の歴史 地図製作 Gis開発の 株式会社 中央ジオマチックス
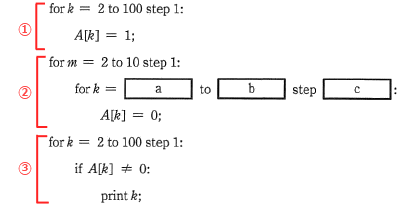



平成25年春期問7 ループの初期値 終値 増分 応用情報技術者試験 Com




Haskell 素数判定 試し割り エラトステネスの篩 Web備忘録



素数を羅列するプログラム ましろのログ




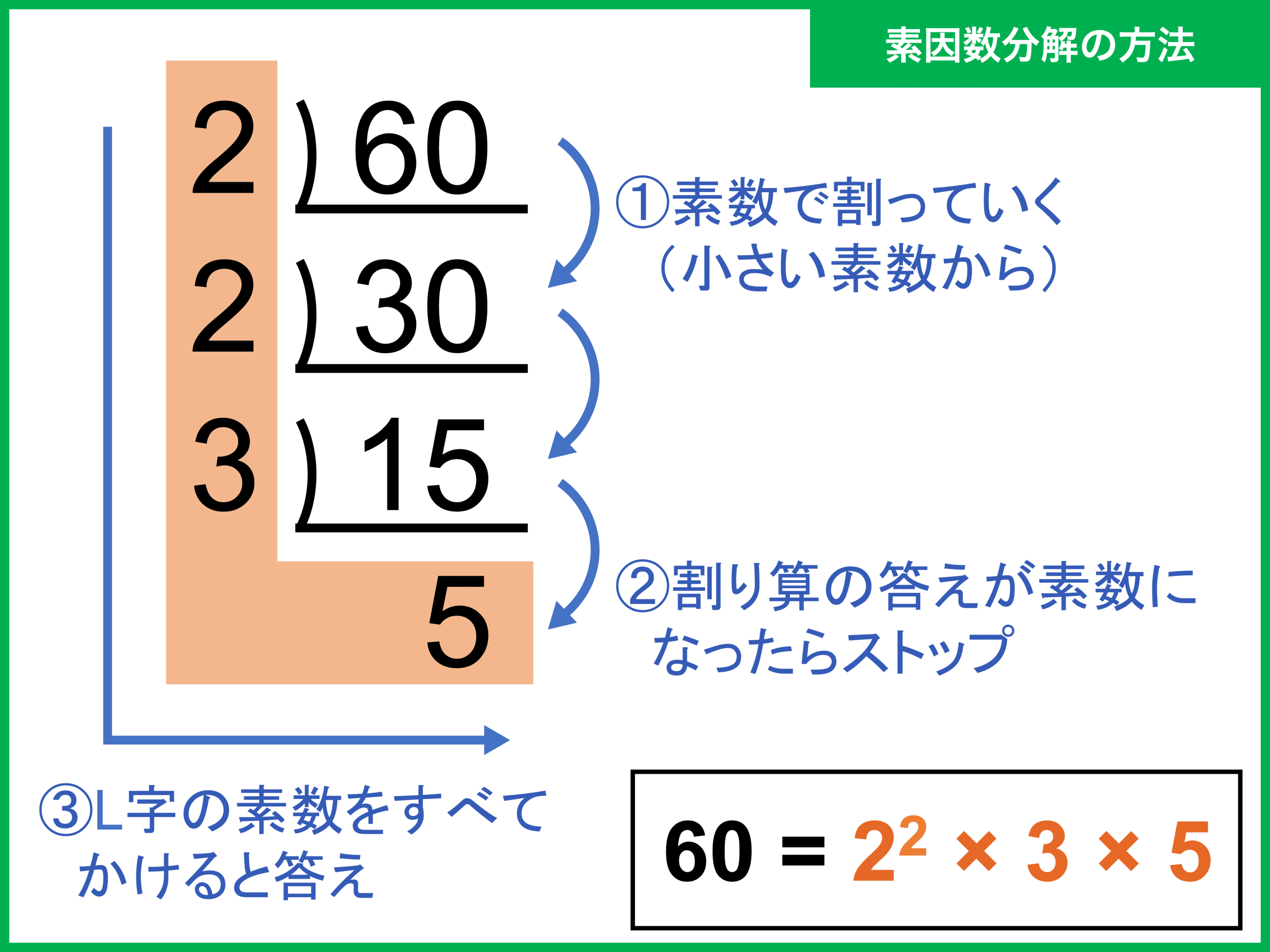
素数 素因数分解 算数用語集




おおい町暦会館 展示資料の紹介
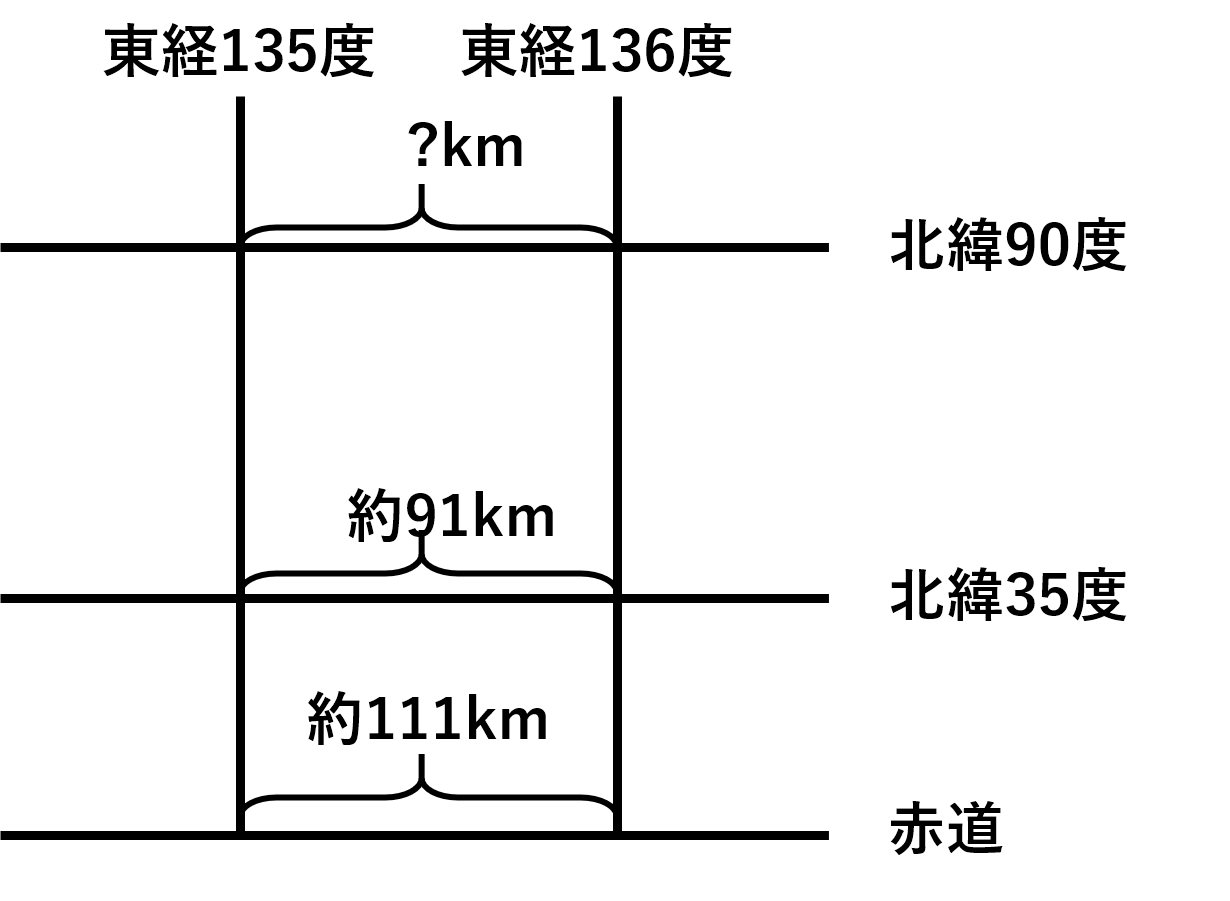



緯度 経度の 1度はどれくらいの長さがあるのか Wingfield Since1981



Algorithm C




Prime Wolfram言語ドキュメント




エラトステネスとはどんな人物 簡単に説明 完全版まとめ 歴史上の人物 Com




数学的帰納法によるプログラミングを修得するためにf 代数を攻略する Bitterharvest S Diary




素数 たかしの愛した算数学




Haskell 素数判定 試し割り エラトステネスの篩 Web備忘録




第1節 地球の概観



エラトステネスのふるい




数学的帰納法によるプログラミングを修得するためにf 代数を攻略する Bitterharvest S Diary



年03月 令和元年 から のプログラミング




Concurrent Prologのオリジナルtシャツ オリジナルtシャツを簡単自作 無料販売budgets 最安値



地球の概観



年03月 令和元年 から のプログラミング



Algorithm C
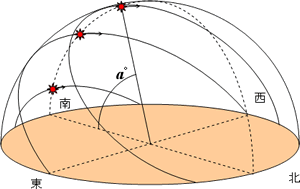



地球を測 はか る 科学夜話 学びの場 Com




ピラミッド計算その4 Sakurai Susumu Website



地図と一秒の世界



素数




測地学 Wikipedia



地図と一秒の世界




中学受験算数 素数を見つけろ 超便利技 エラトステネスの篩 って知ってる 毎日1題中学受験算数27 セミナー好き家庭教師の有益な情報発信部屋




数学的帰納法によるプログラミングを修得するためにf 代数を攻略する Bitterharvest S Diary
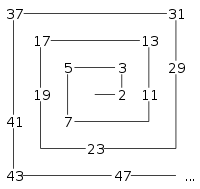



素数 たかしの愛した算数学




第1節 地球の概観
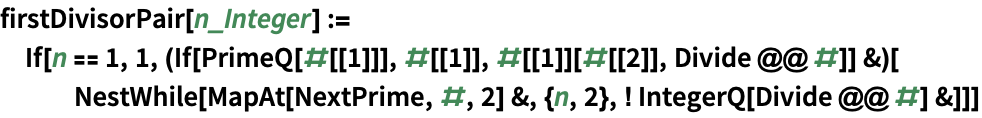



Prime Wolfram言語ドキュメント




中学数学 負の数を1 理解できる3つのストーリー Qikeru 学びを楽しくわかりやすく




素因数分解とrsa 叡智の三猿



整数 発展問題1 解答 学ぶ 教える Com
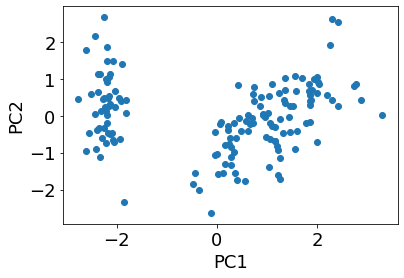



年03月 令和元年 から のプログラミング



無限リストによるエラトステネスのふるい Qiita




地球の直径を日本で初めて割り出した意外な人物 宇宙の星雲 惑星など ワクワクする楽しみ方




おおい町暦会館 展示資料の紹介




Primepi Wolfram言語ドキュメント
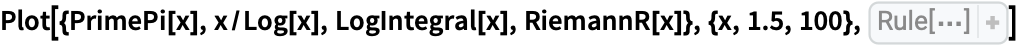



Primepi Wolfram言語ドキュメント




数学的帰納法によるプログラミングを修得するためにf 代数を攻略する Bitterharvest S Diary



地図の歴史 古代




ミンナノヒーローの掲示板 競走馬データ Netkeiba Com




中学受験算数 素数を見つけろ 超便利技 エラトステネスの篩 って知ってる 毎日1題中学受験算数27 セミナー好き家庭教師の有益な情報発信部屋



地図と一秒の世界
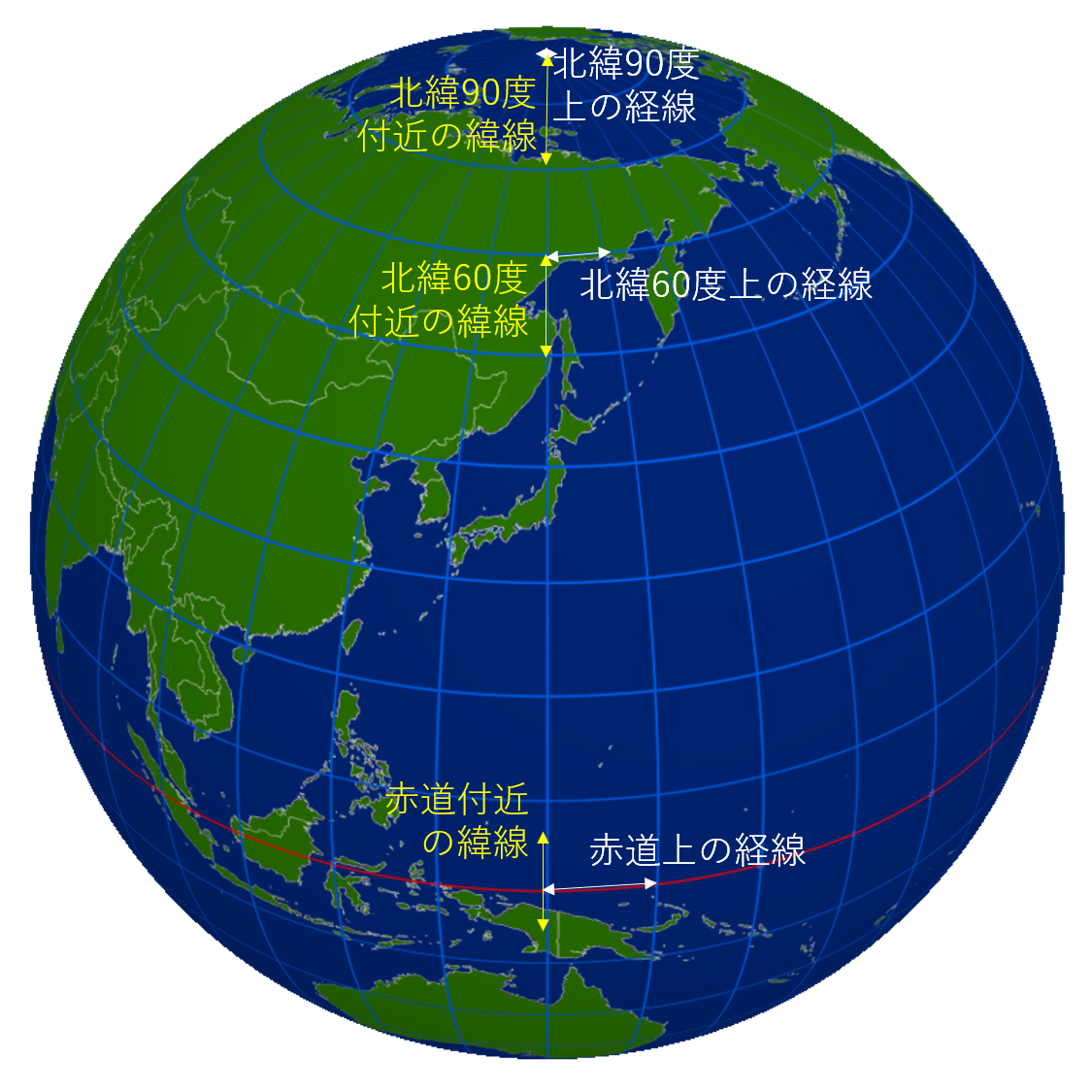



緯度 経度の 1度はどれくらいの長さがあるのか Wingfield Since1981



エラトステネスの子午線測定 山岡の地理b準備室



地球の概観




収蔵品 おおい町暦会館


0 件のコメント:
コメントを投稿